The Pythagorean Theorem And Its Converse Answers

The pythagorean theorem and its converse answers – The Pythagorean theorem and its converse, fundamental principles in geometry, provide invaluable tools for understanding and solving problems involving right triangles. This theorem has fascinated mathematicians and scientists for centuries, with its applications extending far beyond the classroom.

In this comprehensive guide, we will explore the Pythagorean theorem, its converse, and their practical applications. We will delve into the historical context of these theorems, examine their mathematical proofs, and uncover their significance in various fields.

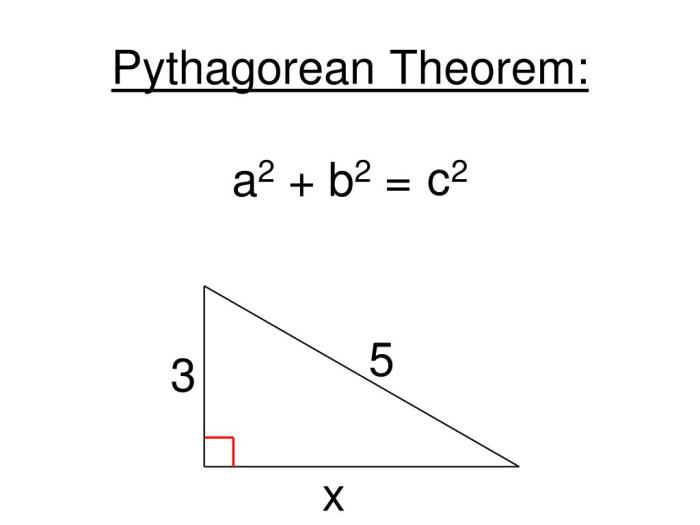
Pythagorean Theorem

The Pythagorean theorem is a fundamental relation in Euclidean geometry that states that in a right triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides.

In other words, if a, b, and care the lengths of the sides of a right triangle, with cbeing the hypotenuse, then the Pythagorean theorem can be expressed as:

a²+ b ²= c ²

Examples of the Pythagorean Theorem in Real-Life Scenarios

In architecture, the Pythagorean theorem is used to calculate the length of roof rafters, stairs, and other structural elements.
In engineering, the Pythagorean theorem is used to determine the forces acting on beams, bridges, and other structures.
In surveying, the Pythagorean theorem is used to measure distances and heights indirectly.

Converse of the Pythagorean Theorem: The Pythagorean Theorem And Its Converse Answers

The converse of the Pythagorean theorem states that if the square of the length of one side of a triangle is equal to the sum of the squares of the lengths of the other two sides, then the triangle is a right triangle.

In other words, if a, b, and care the lengths of the sides of a triangle, and a²+ b ²= c ², then the triangle is a right triangle.

Demonstrating the Converse of the Pythagorean Theorem

To demonstrate the converse of the Pythagorean theorem, we can use the following steps:

Let a, b, and cbe the lengths of the sides of a triangle, with cbeing the longest side.
If a²+ b ²= c ², then we can use the Pythagorean theorem to conclude that the triangle is a right triangle.
If a²+ b ²≠ c ², then the triangle is not a right triangle.

Applications of the Pythagorean Theorem and its Converse

Applications in Architecture, Engineering, and Surveying

In architecture, the Pythagorean theorem is used to calculate the length of roof rafters, stairs, and other structural elements.
In engineering, the Pythagorean theorem is used to determine the forces acting on beams, bridges, and other structures.
In surveying, the Pythagorean theorem is used to measure distances and heights indirectly.

Applications in Geometry, The pythagorean theorem and its converse answers

The converse of the Pythagorean theorem is used to classify triangles as right triangles, obtuse triangles, or acute triangles.
The Pythagorean theorem can also be used to find the length of the altitude of a right triangle.

Historical Context

The Pythagorean theorem is named after the Greek mathematician Pythagoras, who is credited with its discovery around 530 BC.

However, there is evidence that the theorem was known to Babylonian mathematicians as early as 1800 BC.

Over the centuries, the Pythagorean theorem has been proved in many different ways, including geometric proofs, algebraic proofs, and trigonometric proofs.

Mathematical Proofs

Proof of the Pythagorean Theorem

There are many different proofs of the Pythagorean theorem, but one of the most common is the geometric proof:

Let a, b, and cbe the lengths of the sides of a right triangle, with cbeing the hypotenuse.
Construct a square with side length c.
Inside the square, construct four right triangles, each with sides a, b, and c.
The area of the square is c².
The area of each of the four right triangles is (ab)/2.
Therefore, the area of the four right triangles is 4(ab)/2 = 2ab.
Since the area of the square is equal to the sum of the areas of the four right triangles, we have:

c²= 2ab
Solving for c, we get:

c = √(2ab)
Squaring both sides, we get:

c²= 2ab
Which is the Pythagorean theorem.

Query Resolution

What is the Pythagorean theorem?

The Pythagorean theorem states that in a right triangle, the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides.

What is the converse of the Pythagorean theorem?

The converse of the Pythagorean theorem states that if the square of one side of a triangle is equal to the sum of the squares of the other two sides, then the triangle is a right triangle.

How is the Pythagorean theorem used in real life?

The Pythagorean theorem has applications in various fields, including architecture, engineering, surveying, and navigation. It is used to calculate distances, heights, and angles in practical situations.